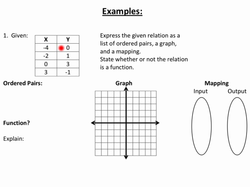
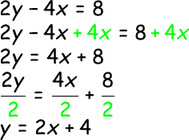RELATIONS
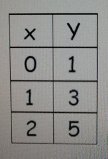
A relation can be represented in many ways: (If the x does not repeat, then the relation is a FUNCTION)
FUNCTIONS
A FUNCTION is a relation where each x goes to only one y. In other words, the x does not repeat. It will pass the vertical line test and each x has only one y.
Determining if a relation is a function:
ordered pairs: Look at the x values (the first coordinate in the ordered pair), do any of the x's repeat? If they do, it is NOT a function.
Tables: Look at the x values (left side), do any of the x values repeat? If they do, it is NOT a function.
Mappings: Look at the x values (left oval), do any of the x values have two lines - drawn to two different y values?: If they do, it is NOT a function
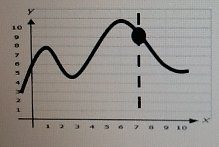
Graphs: Does it pass the vertical line test? If you draw a vertical line, will it cross the graph only once? Then it IS a function.
ACTIVITY: Is it a Function??
ordered pairs: Look at the x values (the first coordinate in the ordered pair), do any of the x's repeat? If they do, it is NOT a function.
Tables: Look at the x values (left side), do any of the x values repeat? If they do, it is NOT a function.
Mappings: Look at the x values (left oval), do any of the x values have two lines - drawn to two different y values?: If they do, it is NOT a function
Graphs: Does it pass the vertical line test? If you draw a vertical line, will it cross the graph only once? Then it IS a function.
ACTIVITY: Is it a Function??
PROPERTIES

Commutative Property (order does not matter) (a)(b) = (b)(a) and a + b = b + a
Associative Property (grouping does not matter) (ab)c = a(bc) and (a + b) + c = a + (b + c)
Distributive Property a (b + c) = ab + ac
Activity: Name the Property
Associative Property (grouping does not matter) (ab)c = a(bc) and (a + b) + c = a + (b + c)
Distributive Property a (b + c) = ab + ac
Activity: Name the Property
y = mx + b (Slope intercept Form) ...the equation for a line
- y: y is the DEPENDENT variable, the y values are the RANGE, y is also known as f(x), the 2nd coordinate in an ordered pair (__, y)
m: m is the slope, the rate of change, the change in y over the change in x, rise/run, y2-y1/x2-x1
x: x is the INDEPENDENT variable, the x values are the DOMAIN, fir first coordinte in an ordered pair (x, ___)
b: b is the y-intercept. (0, b), where the line crosses the y-axis, where x is 0, the starting point, beginning value, the constant

SCATTERPLOTS
A SCATTERPLOT is a graph in which two sets of data are plotted on a coordinate plane
Scatterplots are used to investigate a relationship between 2 quantities and to make predictions
The independent variable belongs on the x-axis and the dependent variable belongs on the y-axis.
Scatterplots will have a positive correlation, negative correlation or no correlation
The trend line goes right through the midst of the points. It is used to make predictions.
Scatterplots are used to investigate a relationship between 2 quantities and to make predictions
The independent variable belongs on the x-axis and the dependent variable belongs on the y-axis.
Scatterplots will have a positive correlation, negative correlation or no correlation
The trend line goes right through the midst of the points. It is used to make predictions.

Scatterplots flashcards

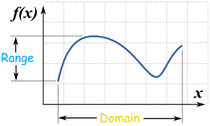
DOMAIN AND RANGE
DOMAIN: the set of all possible x values
RANGE: the set of all possible y values
DoLoR the RoBoT (Domain: from Left to Right, Range: from Bottom to Top)
RANGE: the set of all possible y values
DoLoR the RoBoT (Domain: from Left to Right, Range: from Bottom to Top)


Continuous functions:
no breaks in the graph (it includes fractional values)
it is measured
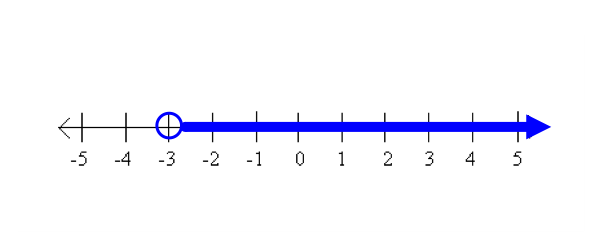
Use < unless its an open cirlce or infinity, then use <
Domain: -8 < x < 6 and Range: -8 < y < 6
it is measured
Use < unless its an open cirlce or infinity, then use <
Domain: -8 < x < 6 and Range: -8 < y < 6
Discrete functions:

the graph consists of separate points (it only includes whole number values)
it is counted
Domain: { -2, -1, 6} and Range: {3, 1, 5}
it is counted
Domain: { -2, -1, 6} and Range: {3, 1, 5}
SOLVING FOR X
First you box the variable, cancel what's beside it, divide by what's inside the box, Reduce and you've solved it.
To Solve for x:
1) Simplify both sides (distribute and combine like terms)
2) Cancel the Little Guy (cancel the smaller x if there are x's on both side of the equal sign)
3) Box the variable and solve for x. (Box, Cancel, Divide)
ACTIVITY: Find the Like Terms
To Solve for x:
1) Simplify both sides (distribute and combine like terms)
2) Cancel the Little Guy (cancel the smaller x if there are x's on both side of the equal sign)
3) Box the variable and solve for x. (Box, Cancel, Divide)
ACTIVITY: Find the Like Terms

SOLVING FOR Y (WRITE IN SLOPE INTERCEPT FORM)

1) BOX THE Y (include the coefficient and its sign)
2) CANCEL WHAT'S BESIDE IT (Cancel term next to box - only combine LIKE terms)
3) DIVIDE BY WHAT'S INSIDE THE BOX (Divide everywhere)
Equations need to be in slope-intercept form (solved for y) in order to identify the slope and y-intercept
OR to put into the [y=] part of the calculator
2) CANCEL WHAT'S BESIDE IT (Cancel term next to box - only combine LIKE terms)
3) DIVIDE BY WHAT'S INSIDE THE BOX (Divide everywhere)
Equations need to be in slope-intercept form (solved for y) in order to identify the slope and y-intercept
OR to put into the [y=] part of the calculator
SLOPE - measures the steepness of a line
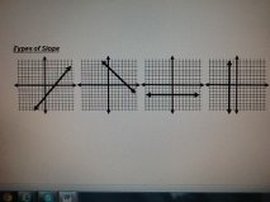
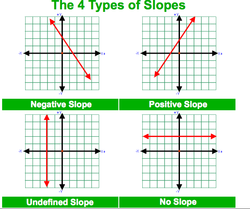
KINDS OF SLOPE
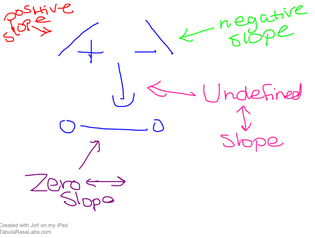
Positive Slope: it goes up and to the right
Negative Slope: it goes down and to the right
Zero Slope: horizontal lines, the equations only have y (ex. y = 4)
Undefined slope: vertical lines, the equations only have x (ex. x = 4)
THE SIGN OF THE SLOPE (the sign on m) DETERMINES IF IT IS POSTIVE OR NEGATIVE)
Steepness of Slope
The coefficient fo x (ignoring the sign) (So the ABSOLUTE VALUE OF THE SLOPE) tells is the line is steep or flat
If m is bigger than 1, it is STEEPER than the parent function (the bigger the number, the steeper the line)
If m is between 0 and 1, it is FLATTER than the parent function (the smaller the fractionm the flatter the line)
If m is bigger than 1, it is STEEPER than the parent function (the bigger the number, the steeper the line)
If m is between 0 and 1, it is FLATTER than the parent function (the smaller the fractionm the flatter the line)
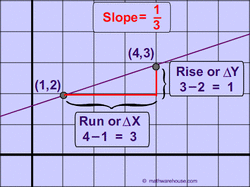
Finding Slope from a graph
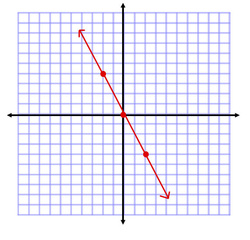
Finding the slope from a graph
1. locate two points on the line
2. Count the slope (moving from one point another)
count the rise (up is positive, down is negative)
count the run (right is positive, left is negative)
3. m = rise/run (write answer as a fraction)
<-- in this example, the slope is (down 4, right 2) or -4/2 which reduces to -2.
Remember:
If the line is horizontal, the slope is 0
If the line is vertical, the slope is undefined
1. locate two points on the line
2. Count the slope (moving from one point another)
count the rise (up is positive, down is negative)
count the run (right is positive, left is negative)
3. m = rise/run (write answer as a fraction)
<-- in this example, the slope is (down 4, right 2) or -4/2 which reduces to -2.
Remember:
If the line is horizontal, the slope is 0
If the line is vertical, the slope is undefined
Video! FINDING SLOPE FROM A GRAPH
Finding Slope from two points
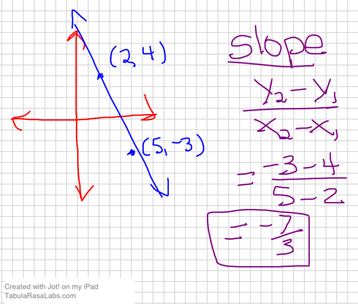
Method 1: Use the Slope Formula---------------(remember the song! "Slope is, y2 minus y1....)--------------- > Label your points with x1, y1 and x2, y2
Plug values into formula and solve
Method 2:
Use the Calculator:
Use STAT. Put x values in L1 and y values in L2
STAT, Calc, 4, enter, enter
The slope will be the "a" value

Slope from an Equation

To identify the slope in an equation, it must be in slope intercept form
1. Solve the equation for y
Box y
cancel what's beside it (only combine like terms!)
cancel by whats in box (divide everywhere!)
2. Identify slope by looking at the coefficient of x.
1. Solve the equation for y
Box y
cancel what's beside it (only combine like terms!)
cancel by whats in box (divide everywhere!)
2. Identify slope by looking at the coefficient of x.
VIDEO! Slope Intercept Form (finding m and b and graphing from an equation)
PARALLEL AND PERPENDICULAR
To determine if two lines are parallel or perpendicular:
Put the equations in Slope-Intercept Form (y=mx+b) (Solve for y) and compare the slopes
If the slopes are the same, the lines are parallel
If the slopes are negative reciprocals, the lines are perpendicular
Negative Reciprocals:
The signs are opposite from each other (one is positive and one is negative)
The numbers are reciprocals of each other
Put the equations in Slope-Intercept Form (y=mx+b) (Solve for y) and compare the slopes
If the slopes are the same, the lines are parallel
If the slopes are negative reciprocals, the lines are perpendicular
Negative Reciprocals:
The signs are opposite from each other (one is positive and one is negative)
The numbers are reciprocals of each other
POINT SLOPE FORM

Use POINT SLOPE FORM when you are given a point and the slope.
(sometimes you need to figure out the slope!)
1. Plug in your point (put your x value in for x1 and your y value in for y1. (leave the other x and y alone)
2. Plug in your slope for m
3. Solve for y. (distribute, the box your y and cancel what's beside it - combine like terms!)
(sometimes you need to figure out the slope!)
1. Plug in your point (put your x value in for x1 and your y value in for y1. (leave the other x and y alone)
2. Plug in your slope for m
3. Solve for y. (distribute, the box your y and cancel what's beside it - combine like terms!)
Video! Point Slope Form
X AND Y INTERCEPTS
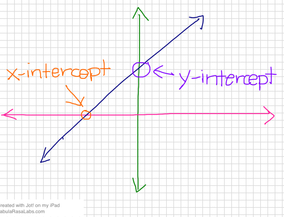
X INTERCEPTS
x-intercepts always have y = 0. (x, 0)
x-intercepts are the solutions to the equations
Y INTERCEPTS
y-intercepts always have x = 0. (0, y)
y-intercepts are the starting points & the "b" in the equation, y = mx + b
Finding the x-intercept
Plug 0 in for y and solve for x
Finding the y-intercept
Plug 0 in for x and solve for y.
x-intercepts always have y = 0. (x, 0)
x-intercepts are the solutions to the equations
Y INTERCEPTS
y-intercepts always have x = 0. (0, y)
y-intercepts are the starting points & the "b" in the equation, y = mx + b
Finding the x-intercept
Plug 0 in for y and solve for x
Finding the y-intercept
Plug 0 in for x and solve for y.
VIDEO! Finding the x-intercept
VIDEO! Finding the y-intercept
DIRECT VARIATION
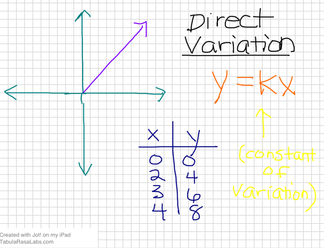
y varies directly with x. y = kx where k is the constant of variation
Recognizing Direct Variation:
The graph of direct variation is a straight, diagonal line goes through the origin.
A table, divide y/x and get the same value (k) each time, its direct variation
Solving with DIRECT VARIATION
When given an x and y: Divide y/x for the constant of variation (k)
When given 3 values (3 numbers): Solve using PROPORTION (butterfly)
Recognizing Direct Variation:
The graph of direct variation is a straight, diagonal line goes through the origin.
A table, divide y/x and get the same value (k) each time, its direct variation
Solving with DIRECT VARIATION
When given an x and y: Divide y/x for the constant of variation (k)
When given 3 values (3 numbers): Solve using PROPORTION (butterfly)
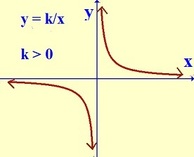
INVERSE VARIATION
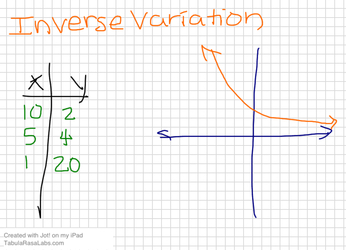
y varies inversely with x. y = k/x where k is the constant of variation
Recognizing Inverse Variation:
The graph of inverse variation is a curve that gets close, but
never touches the x axis or y axis.
A table, multiply x and y and get the same value (k) each time, its inverse
Solving with INVERSE VARIATION
When given x and y: Multiply (x)(y) for the constant of variation(k)
When given 3 values (3 numbers): solve using
INVERSE PROPORTION (set up proportion with multiplication instead of division: xy = xy.
Recognizing Inverse Variation:
The graph of inverse variation is a curve that gets close, but
never touches the x axis or y axis.
A table, multiply x and y and get the same value (k) each time, its inverse
Solving with INVERSE VARIATION
When given x and y: Multiply (x)(y) for the constant of variation(k)
When given 3 values (3 numbers): solve using
INVERSE PROPORTION (set up proportion with multiplication instead of division: xy = xy.
SYSTEMS OF EQUATIONS
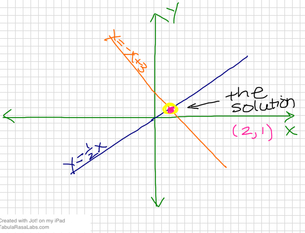
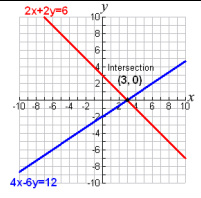
a SYSTEM of equations is two or more equations working together.
The solution will be the intersection of the two lines.
A system of equation can be solved using a calculator, by graphing, by substitution and by elimination
Solving a System of Equation in the CALCULATOR
1. type both equations into [y=] (both equations must first be solved for y)
2. 2nd, trace, 5, enter, enter, enter
Writing a System from a word problem
1. Assign the variables
2, work one sentence at a time to write the information algebraically
Example: Four pickles and two nachos cost $10. (4P + 2N = 10)
If two thing are being compared - start with bigger one
Example: Hamburgers are $4 more than French Fries (h = F + 4)
The solution will be the intersection of the two lines.
A system of equation can be solved using a calculator, by graphing, by substitution and by elimination
Solving a System of Equation in the CALCULATOR
1. type both equations into [y=] (both equations must first be solved for y)
2. 2nd, trace, 5, enter, enter, enter
Writing a System from a word problem
1. Assign the variables
2, work one sentence at a time to write the information algebraically
Example: Four pickles and two nachos cost $10. (4P + 2N = 10)
If two thing are being compared - start with bigger one
Example: Hamburgers are $4 more than French Fries (h = F + 4)
VIDEO!! Writing Systems of Equations
VIDEO! Solving a System by Substitution
VIDEO! Solving a System by Graphing
VIDEO! Solving a System by Substitution
VIDEO! Solving a System by Graphing
INEQUALITIES

1) solve the inequatlity for y (if you multiply or divide by a negative, FLIP the inequality sign)
2) draw the line using slope and y-intercept
3) the line will be dashed if it is < or >
the line will be solid if it is < or >
4) shade above the line if the inequality is > or >
shade below th eline is the inequality is < or <
2) draw the line using slope and y-intercept
3) the line will be dashed if it is < or >
the line will be solid if it is < or >
4) shade above the line if the inequality is > or >
shade below th eline is the inequality is < or <
EXPONENTS

Adding or Subtracting Exponents: no changes in exponents (its combining like terms)
Multiplying Exponents: Multiply the coefficients and ADD the EXPONENTS
Dividing Exponents: Divide tghe coefficients and SUBTRACT the EXPONENTS
Power to Power (exponent to exponent): MULTIPLY the EXPONENTS
Multiplying Exponents: Multiply the coefficients and ADD the EXPONENTS
Dividing Exponents: Divide tghe coefficients and SUBTRACT the EXPONENTS
Power to Power (exponent to exponent): MULTIPLY the EXPONENTS
MULTIPLYING BINOMIALS
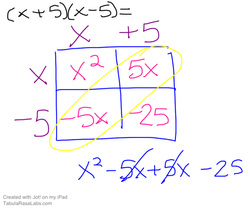
Multiplying Binomials by Box Method
1) multiply to fill in boxes
2) combine like terms (usually found on the diagonal)
<----- the answer: x^2 - 25 (the 5x and -5x cancelled)
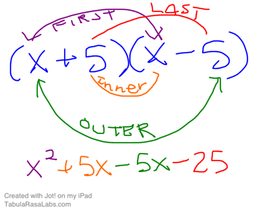
Multipying Binomials by FOIL Method
1) multiply the frist tersm, the outer terms, the inner terms and the last terms
2) combine like terms (usually the inner and outer terms)
1) multiply to fill in boxes
2) combine like terms (usually found on the diagonal)
<----- the answer: x^2 - 25 (the 5x and -5x cancelled)
Multipying Binomials by FOIL Method
1) multiply the frist tersm, the outer terms, the inner terms and the last terms
2) combine like terms (usually the inner and outer terms)
VIDEO: MULTIPLYING BINOMIALS
multiplying binomials practice

FACTORING GCF
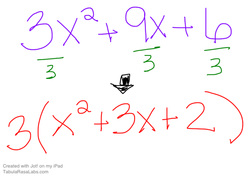
Find the largest term that will divide evenly into all terms
the GCF of 14ac - 6ab is 2a since 2a is the largest term that will divide into 14ab and 6ab evenly
Now divide each term by the GCF.
14ac– 6ab = 2a(7c - 3b)
the GCF of 14ac - 6ab is 2a since 2a is the largest term that will divide into 14ab and 6ab evenly
Now divide each term by the GCF.
14ac– 6ab = 2a(7c - 3b)

FACTORING TRINOMIALS
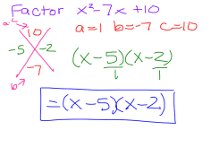
1) label a, b, and c
2) put (a)(c) in the top of the X and b in the bottom
3) find the factors that will multiply to the top number and add to the bottom number
4) rewrite the equation using the two new factors for the middle term
5) factor the GCF from the first two terms (factor a negative if x is negative)
6) factor the GF from the last two terms (factor a negative if x is negative)
7) Factor the matching parenthesis (the GCF of the two remaining terms)
2) put (a)(c) in the top of the X and b in the bottom
3) find the factors that will multiply to the top number and add to the bottom number
4) rewrite the equation using the two new factors for the middle term
5) factor the GCF from the first two terms (factor a negative if x is negative)
6) factor the GF from the last two terms (factor a negative if x is negative)
7) Factor the matching parenthesis (the GCF of the two remaining terms)

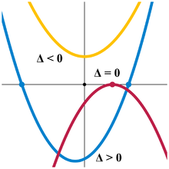
QUADRATICS
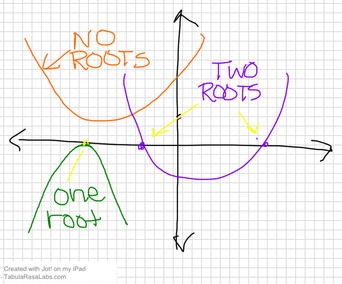
y = ax^2 + bx + c
it opens up if a is positive, it opens down if a is negative
if it opens up, the vertex is a minimum
if it opens down, the vertex is a maximum
if |a| > 1, then the parabola is narrow
if 0 < |a| < 1 (a fraction) then the parabola is wide
c is the y-intercept (0, c) (translating is sliding the parabola up or downt he y-axis)
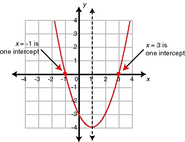
the solutions (also called roots and zeros) are the x-intercepts
There can be two, one or no solutions
it opens up if a is positive, it opens down if a is negative
if it opens up, the vertex is a minimum
if it opens down, the vertex is a maximum
if |a| > 1, then the parabola is narrow
if 0 < |a| < 1 (a fraction) then the parabola is wide
c is the y-intercept (0, c) (translating is sliding the parabola up or downt he y-axis)
the solutions (also called roots and zeros) are the x-intercepts
There can be two, one or no solutions


Solving Quadratics

Set equation equal to y or 0
factor , then set each factor equal to zero and solve.
OR
solve for y (or 0) and type into y=
then type 0 in y=
2nd, trace, 5, move cursor to x-intercept and enter, enter, enter (repeat for other x-intercept)
factor , then set each factor equal to zero and solve.
OR
solve for y (or 0) and type into y=
then type 0 in y=
2nd, trace, 5, move cursor to x-intercept and enter, enter, enter (repeat for other x-intercept)


QUADRATIC FORMULA
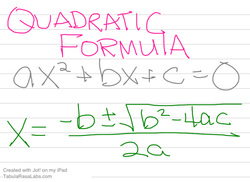
solve the equation for y (or 0)
label a, b, and c
plug in to formula and simplify
label a, b, and c
plug in to formula and simplify

EXPONENTIAL GROWTH AND DECAY

Exponential Growth: (grows quickly)
as x increases. y increases.
to find b, 1 + rate
Exponential Decay: (decreases quickly)
as x increases, y decreases.
to find b, 1 - rate
as x increases. y increases.
to find b, 1 + rate
Exponential Decay: (decreases quickly)
as x increases, y decreases.
to find b, 1 - rate

Solving Quadratics by graphs, tables and concrete models
homework
video - solve quadratics by graphs, tables and concrete models
homework
video - solve quadratics by graphs, tables and concrete models
Solving Quadratics by Quadratic Formula
homework
video - solve quadratics by quadratic formula
Form - Complete this form after viewing the video
Form - Complete this form after watching the video
homework
video - solve quadratics by quadratic formula
Form - Complete this form after viewing the video
Form - Complete this form after watching the video
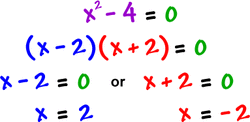
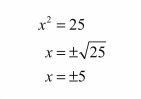






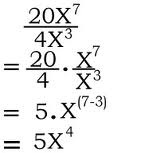


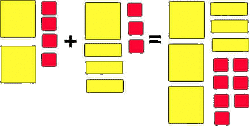
Solve Systems of Equations Using Concrete Models
VIDEO: Solve Systems using Concrete Models (youtube)
Homework
VIDEO: Solve Systems using Concrete Models (youtube)
Homework




Standard Form
VIDEO: Standard Form
Homework
VIDEO: Standard Form
Homework

Families of Lines
VIDEO: Families of Lines
Homework
VIDEO: Families of Lines
Homework
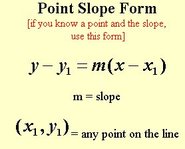
Point Slope Form
VIDEO: Point Slope Form
Homework : Day 1
Homework: Day 2
VIDEO: Point Slope Form
Homework : Day 1
Homework: Day 2

Direct Variation
VIDEO: Direct Variation
Homework
VIDEO: Direct Variation
Homework
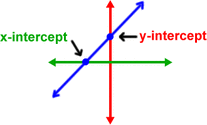
x and y Intercepts
VIDEO: x and y Intercepts
Homework
VIDEO: x and y Intercepts
Homework
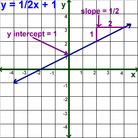
Graphing Equations in Slope-Intercept Form
VIDEO: Graphing Equations in Slope-Intercept Form
Homework
VIDEO: Graphing Equations in Slope-Intercept Form
Homework
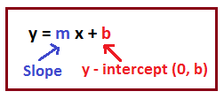
Solve for y (Slope Intercept Form)
VIDEO: Solve for y
Homework - Day 1
Homework - Day 2
VIDEO: Solve for y
Homework - Day 1
Homework - Day 2
Slope Project
Before the Project Information
The Project
Before the Project Information
The Project

Multiple Representations and Evaluating a Function
VIDEO: Multiple Representations
VIDEO: Evaluating a Function
Homework
VIDEO: Multiple Representations
VIDEO: Evaluating a Function
Homework


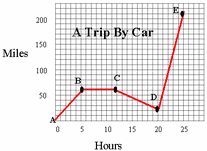

First Six Weeks Test REVIEW
homework
homework

First Six Week's Skillbuiders
Skillbuilder 1 homework
Skillbuilder 2 homework
Skillbuilder 3 homework
Skillbuilder 1 homework
Skillbuilder 2 homework
Skillbuilder 3 homework

Solving Applications
homework
homework
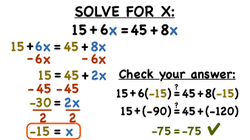
Solving Equations with Variables on Both Sides
VIDEO: Solving Equations with Variables on Both Sides
Homework
VIDEO: Solving Equations with Variables on Both Sides
Homework


Solving Two Step Equations
VIDEO: Solving Two Step Equations
Homework
Song - Solving an Equation (Pop! Goes the Weasel)
Vocabulary
VIDEO: Solving Two Step Equations
Homework
Song - Solving an Equation (Pop! Goes the Weasel)
Vocabulary

Combine Like Terms
VIDEO: Combine Like Terms
Homework
Vocabulary
Find the Like Terms
Combine like terms - Practice (flashcards, matching...)
VIDEO: Combine Like Terms
Homework
Vocabulary
Find the Like Terms
Combine like terms - Practice (flashcards, matching...)
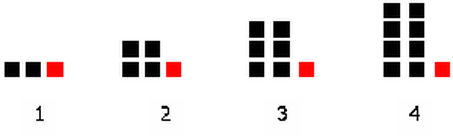
Patterns
VIDEO: Patterns
VIDEO: Patterns into a Table
VIDEO: Pattern to an Expressions
Homework
Vocabulary
VIDEO: Patterns
VIDEO: Patterns into a Table
VIDEO: Pattern to an Expressions
Homework
Vocabulary
Variables and Evaluating Expressions
VIDEO: Variables and Evaluating Expressions
Homework
Vocabulary
Phrase Sort
VIDEO: Variables and Evaluating Expressions
Homework
Vocabulary
Phrase Sort
Scatterplots
VIDEO: Scatterplots
Homework
Vocabulary
VIDEO: Scatterplots
Homework
Vocabulary
|
Integers
VIDEO - Integers Homework |